Stack详解

基于JDK8

1、栈数据结构动画演示

从动画中可以看出，栈这种数据结构 只能从同一头进，从同一头出。
比较正式的说法叫： 后进先出（LIFO, Last In First Out）。

2、Stack的继承体系

public class Stack<E> extends Vector<E>

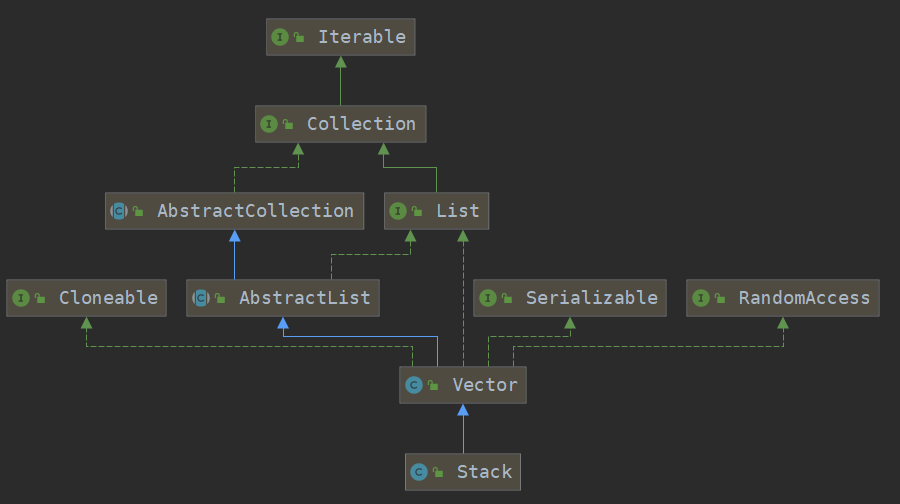
可以看到JDK提供的 Stack 是利用 Vector实现的。所以Stack 类也是线程安全的。

3、Stack的push (入栈)方法

public E push(E item) {
    // 调用 addElement 方法将 item 添加到 Vector 的末尾
    addElement(item);

    // 返回被添加的元素 item
    return item;
}

public synchronized void addElement(E obj) {
    // 修改计数器增加，用于记录 Vector 被修改的次数
    modCount++;

    // 确保 Vector 有足够的容量来容纳新元素
    ensureCapacityHelper(elementCount + 1);

    // 将新元素添加到 elementData 数组的 elementCount 位置
    elementData[elementCount++] = obj;
}

private void ensureCapacityHelper(int minCapacity) {
    // 检查是否需要扩容，如果当前容量小于 minCapacity 则进行扩容
    if (minCapacity - elementData.length > 0)
        grow(minCapacity);
}

protected Object[] elementData;

private void grow(int minCapacity) {
    // 当前数组的容量
    int oldCapacity = elementData.length;

    // 新的容量，如果 capacityIncrement 大于 0 则按此增量扩容，否则容量翻倍
    int newCapacity = oldCapacity + ((capacityIncrement > 0) ? capacityIncrement : oldCapacity);

    // 确保新的容量不小于最小所需的容量
    if (newCapacity - minCapacity < 0)
        newCapacity = minCapacity;

    // 检查新的容量是否超过最大允许的数组大小
    if (newCapacity - MAX_ARRAY_SIZE > 0)
        newCapacity = hugeCapacity(minCapacity);

    // 将元素数组扩容到新的容量
    elementData = Arrays.copyOf(elementData, newCapacity);
}

上面只有push方法是Stack提供的，其余方法都是Vector类提供的。

4、Stack的pop (出栈)方法

public synchronized E pop() {
    E obj;
    int len = size();

    // 获取栈顶元素
    obj = peek();

    // 移除栈顶元素
    removeElementAt(len - 1);

    // 返回被移除的栈顶元素
    return obj;
}

public synchronized E peek() {
    int len = size();

    // 如果栈为空，抛出 EmptyStackException 异常
    if (len == 0)
        throw new EmptyStackException();

    // 返回栈顶元素（位于 elementData 数组的最后一个有效位置）
    return elementAt(len - 1);
}

public synchronized void removeElementAt(int index) {
    // 增加修改计数器
    modCount++;

    // 如果索引超出当前元素数量，抛出 ArrayIndexOutOfBoundsException 异常
    if (index >= elementCount) {
        throw new ArrayIndexOutOfBoundsException(index + " >= " + elementCount);
    }
    // 如果索引为负数，抛出 ArrayIndexOutOfBoundsException 异常
    else if (index < 0) {
        throw new ArrayIndexOutOfBoundsException(index);
    }

    // 计算需要移动的元素个数
    int j = elementCount - index - 1;

    // 如果有需要移动的元素
    if (j > 0) {
        // 将 elementData 数组中 index + 1 到 elementCount - 1 的元素左移一位
        System.arraycopy(elementData, index + 1, elementData, index, j);
    }

    // 减少元素数量
    elementCount--;

    // 将最后一个元素设为 null 以便垃圾回收
    elementData[elementCount] = null;
}

pop (出栈)方法利用到了peek(获取栈顶元素)方法。

5、Stack是如何利用Vector实现栈数据结构的？

上面已经用动画演示了栈数据结构的特点：栈这种数据结构 只能从同一头进，从同一头出。

栈的主要操作包括以下几种：

• 压栈（push）：将元素添加到栈的顶部。
• 出栈（pop）：移除并返回栈顶元素。
• 查看栈顶元素（peek）：返回栈顶元素但不移除它。

Stack 类通过继承 Vector，并添加自己的方法，实现了这些操作。
push 方法
push 方法将元素压入栈顶。它实际上调用了 Vector 的 addElement 方法，将元素添加到 Vector 的末尾。

pop 方法
pop 方法移除并返回栈顶元素。它先调用 peek 方法获取栈顶元素，然后调用 removeElementAt 方法移除该元素。

peek 方法
peek 方法返回栈顶元素但不移除它。它直接访问 Vector 的最后一个元素。

Vector和ArrayList类似，底层都是使用Object数组来存储元素的。
Stack通过操作数组的末尾，比如push只把元素添加到数组的末尾，pop只移除数组末尾的元素。

6、自己实现栈(不借助JDK提供的集合)

主要利用Object 数组和Arrays.copyOf方法

class MyStack<T>{

    // 默认容量
    private final Integer defaultCapacity = 10;
    // 存储元素的数组
    private Object[] elementData;
    // 真正存储的元素个数
    private int elementCount;

    public MyStack() {
        this.elementData = new Object[10];
    }


    public void push(T element){
        // 元素个数大于默认容量就复制数组
        if(gtDefaultCapacity(elementCount + 1)){
            // 创建一个新的数组，长度为当前数组长度加1
            Object[] newElements = Arrays.copyOf(elementData, elementCount + 1);
            newElements[elementCount++] = element;
            elementData = newElements;
        }else {
            // 否则就直接添加元素到数组末尾
            this.elementData[elementCount++] = element;
        }
    }

    // 获取栈顶元素
    @SuppressWarnings(value = "unchecked")
    public T peek(){
        if(elementCount<=0){
            throw new RuntimeException("当前栈为空!");
        }
        return (T)elementData[elementCount-1];
    }

    // 删除栈顶元素
    @SuppressWarnings(value = "unchecked")
    public T pop(){
        if(elementCount<=0){
            throw new RuntimeException("当前栈为空!");
        }
        Object temp = elementData[elementCount - 1];
        elementData = Arrays.copyOf(elementData, elementCount - 1);
        elementCount--;
        return (T) temp;
    }


    // 判断是否大于默认容量
    private boolean gtDefaultCapacity(int length){
        return length > defaultCapacity;
    }

    // 获取栈大小
    public int size(){
        return elementCount;
    }

    // 判断栈是否为空
    public boolean isEmpty(){
        return elementCount <= 0;
    }

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        for (int i =elementCount - 1 ; i >= 0; i--) {
            builder.append(elementData[i].toString()).append("  ");
        }
        return builder.toString();
    }

}

测试：

public static void main(String[] args) throws Exception {
        MyStack<String> myStack = new MyStack<>();
        myStack.push("秀逗");
        myStack.push("四眼");
        myStack.push("大黄");

        System.out.println(myStack.peek());  //  大黄
        System.out.println(myStack.pop());  // 大黄
        System.out.println(myStack.size()); // 2
        System.out.println(myStack.isEmpty()); // false
		System.out.println(myStack);  // 四眼  秀逗

        System.out.println(myStack.pop()); //  四眼  
        System.out.println(myStack.pop());//  秀逗 
        System.out.println(myStack.pop()); // java.lang.RuntimeException: 当前栈为空!
       
    }

我们利用Object 数组和Arrays.copyOf方法实现了一个简单的栈，这个栈包含基本的 push、peek、pop、size、isEmpty方法，并模拟出栈顺序重写了 toString。

7、自己实现栈(借助JDK提供的集合)

上面我们自己利用Object 数组和Arrays.copyOf方法实现了简单的栈，我们默认设置了10的容量，如果超过10个元素，
我们利用Arrays.copyOf完成数组的复制。 这样做是非常耗费性能的，并且我们自己实现的栈是非线程安全的。
下面我们利用JDK现有的集合来实现栈。

利用 ArrayDeque 实现高性能的非线程安全的栈。

class MyStack<T>{
	// 使用 ArrayDeque 作为底层数据结构来存储栈元素
    private ArrayDeque<T> arrayDeque;

	// 构造方法，初始化 ArrayDeque
    public MyStack() {
        this.arrayDeque = new ArrayDeque<T>();
    }
    
	// 将元素压入栈顶，使用 addFirst 方法将元素添加到双端队列的头部
    public void push(T elementData){
        arrayDeque.addFirst(elementData);
    }


    public void peek(){
        arrayDeque.getFirst();
    }

    public T pop(){
       return arrayDeque.removeFirst();
    }

    public int size(){
        return arrayDeque.size();
    }

    public boolean isEmpty(){
        return arrayDeque.isEmpty();
    }

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        // 这里不需要反序迭代  因为我们的push是往头部添加元素 直接正序迭代就是出栈顺序
        Iterator<T> iterator = arrayDeque.iterator();
        while (iterator.hasNext()){
            builder.append(iterator.next().toString()).append("  ");
        }
        return builder.toString();
    }
}

利用 ConcurrentLinkedDeque实现高性能的线程安全的栈。

class MyStack<T>{

    private ConcurrentLinkedDeque<T> concurrentLinkedDeque;

    public MyStack() {
        this.concurrentLinkedDeque = new ConcurrentLinkedDeque<T>();
    }

    public void push(T elementData){
        concurrentLinkedDeque.addFirst(elementData);
    }

    public void peek(){
        concurrentLinkedDeque.getFirst();
    }

    public T pop(){
       return concurrentLinkedDeque.removeFirst();
    }

    public int size(){
        return concurrentLinkedDeque.size();
    }

    public boolean isEmpty(){
        return concurrentLinkedDeque.isEmpty();
    }

    @Override
    public String toString() {
        StringBuilder builder = new StringBuilder();
        // 这里不需要反序迭代  因为我们的push是往头部添加元素 直接正序迭代就是出栈顺序
        Iterator<T> iterator = concurrentLinkedDeque.iterator();
        while (iterator.hasNext()){
            builder.append(iterator.next().toString()).append("  ");
        }
        return builder.toString();
    }
}

ConcurrentLinkedDeque 的高性能线程安全设计，涉及到乐观并发控制策略比如CAS，延迟回收，分段锁等机制。
后面总结并发编程知识的时候再详细分析下ConcurrentLinkedDeque 的设计。

8、栈的应用场景

栈虽然是一种后进先出（LIFO, Last In First Out）的数据结构，但是却有广泛的应用场景。
下面是几个常见的例子：

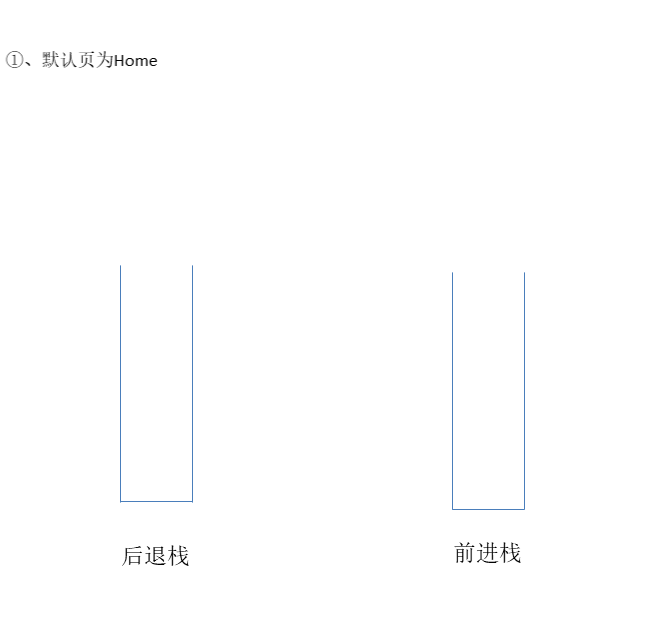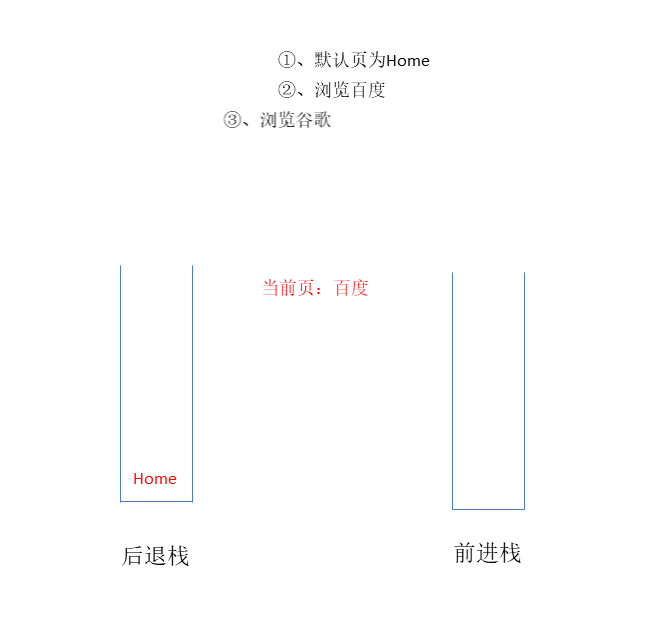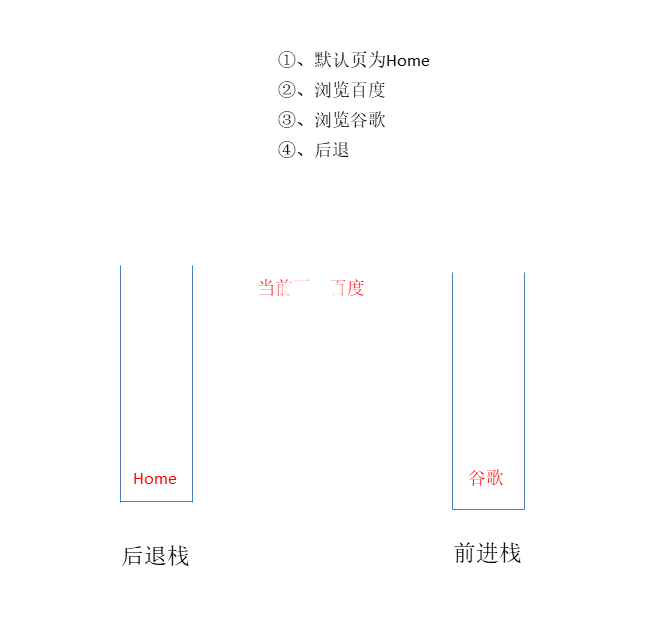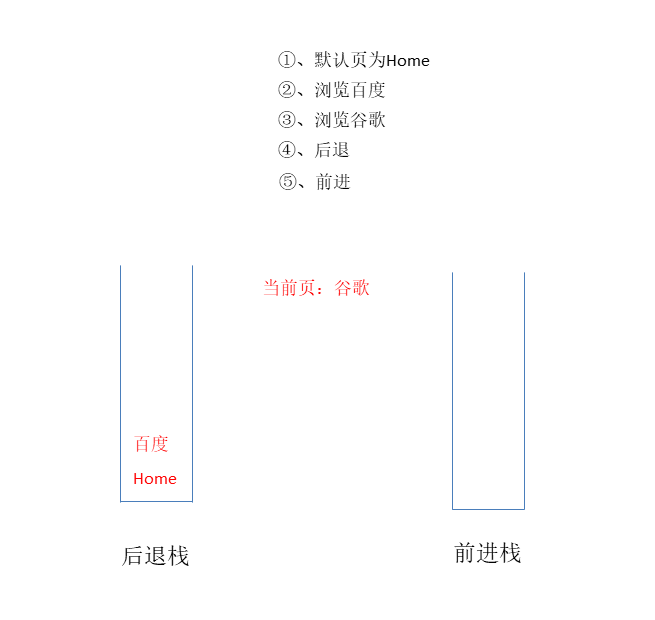
①、浏览器的前进、后退功能实现

可以用两个栈分别存储前进和后退的页面
代码示例：

import java.util.Stack;

public class TestA {
    public static void main(String[] args) {
        Browser browser = new Browser();
        browser.visit("百度");
        browser.visit("谷歌");

        browser.back();  //  百度
        browser.forward();  // 谷歌
    }
}


class Browser {
    // 保存前进页面的栈，用于实现前进功能
    private Stack<String> forwardStack;
    // 保存后退页面的栈，用于实现后退功能
    private Stack<String> backStack;
    // 当前浏览的页面
    private String currentPage;

    // 初始化前进栈、后退栈和当前页面
    public Browser() {
        this.forwardStack = new Stack<>();
        this.backStack = new Stack<>();
        // 初始化默认页面为 "Home"
        this.currentPage = "Home";
    }

    /**
     * 访问新页面
     * @param page 新访问的页面
     */
    public void visit(String page) {
        if (page == null) {
            throw new RuntimeException("页面不能为空");
        }
        // 将当前页面加入后退栈，因为我们将访问新的页面
        backStack.push(currentPage);
        // 更新当前页面为新访问的页面
        currentPage = page;
        // 打印当前浏览页面
        System.out.println("当前浏览页面：" + currentPage);
        // 清空前进栈，因为访问新页面时前进栈失效
        forwardStack.clear();
    }

    /**
     * 前进到下一页面
     */
    public void forward() {
        System.out.println("前进");
        // 如果前进栈不为空
        if (!forwardStack.isEmpty()) {
            // 将当前页面加入后退栈
            backStack.push(currentPage);
            // 从前进栈弹出页面作为当前页面
            currentPage = forwardStack.pop();
            // 打印当前浏览页面
            System.out.println("当前浏览页面：" + currentPage);
        } else {
            // 前进栈为空，无法前进
            System.out.println("当前无前进页面");
        }
    }

    /**
     * 后退到上一页面
     */
    public void back() {
        System.out.println("后退");
        // 如果后退栈不为空
        if (!backStack.isEmpty()) {
            // 将当前页面加入前进栈
            forwardStack.push(currentPage);
            // 从后退栈弹出页面作为当前页面
            currentPage = backStack.pop();
            // 打印当前浏览页面
            System.out.println("当前浏览页面：" + currentPage);
        } else {
            // 后退栈为空，无法后退
            System.out.println("当前无后退页面");
        }
    }

    /**
     * 获取当前浏览的页面
     * @return 当前页面
     */
    public String getCurrentPage() {
        return currentPage;
    }
}

运行结果：

当前浏览页面：百度
当前浏览页面：谷歌
后退
当前浏览页面：百度
前进
当前浏览页面：谷歌

动画示例

②、表达式求值 （实现简单计算器功能）

栈常用于表达式求值，如中缀表达式转后缀表达式（逆波兰表达式）和逆波兰表达式求值。

先了解几个表达式的基本概念：
一般来说，数学表达式的表示方法主要有以下三种：

中缀表达式 (Infix Notation)
前缀表达式 (Prefix Notation) 又叫 波兰式 (Polish Notation)
后缀表达式 (Postfix Notation) 又叫 逆波兰式 (Reverse Polish Notation)

表达式类型	示例	直观性	优先级标识	计算机实现	别名
中缀表达式	(A + B) * C	高	需要括号	复杂	无
前缀表达式	* + A B C	低	不需要	简单	波兰式
后缀表达式	A B + C *	低	不需要	简单	逆波兰式

特点比较：

• 中缀表达式 是我们日常使用的表达方式，运算符位于操作数之间，直观但需要括号来明确优先级，计算机实现较复杂。
• 前缀表达式（波兰式）运算符位于操作数之前，不需要括号来确定优先级，适合树结构计算，计算机实现简单但不直观。
• 后缀表达式（逆波兰式）运算符位于操作数之后，同样不需要括号来确定优先级，适合栈结构计算，计算机实现简单但不直观。

我们可以利用栈实现计算器功能 (实际上就是中缀表达式转后缀表达式,再利用栈实现后缀表达式的计算)：

import java.util.Scanner;
import java.util.Stack;

public class TestA {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        while (true) {
            System.out.print("请输入一个中缀表达式 (输入 'exit' 退出): ");
            String infixExpression = scanner.nextLine();

            if (infixExpression.equalsIgnoreCase("exit")) {
                break; // 输入 'exit' 退出循环
            }

            try {
                String postfixExpression = infixToPostfix(infixExpression);
                System.out.println("后缀表达式: " + postfixExpression);
                double result = evaluatePostfix(postfixExpression);
                if (result % 1 == 0) { // 判断结果是否为整数
                    System.out.println("计算结果: " + (int) result); // 整数结果去掉小数部分
                } else {
                    System.out.println("计算结果: " + result);
                }
            } catch (Exception e) {
                System.out.println("表达式无效: " + e.getMessage());
            }
        }
        scanner.close();
    }

    // 中缀表达式转后缀表达式
    public static String infixToPostfix(String infix) {
        Stack<Character> stack = new Stack<>();
        StringBuilder postfix = new StringBuilder();

        for (int i = 0; i < infix.length(); i++) {
            char ch = infix.charAt(i);

            if (Character.isDigit(ch)) {
                // 处理多位数字和小数
                while (i < infix.length() && (Character.isDigit(infix.charAt(i)) || infix.charAt(i) == '.')) {
                    postfix.append(infix.charAt(i++));
                }
                postfix.append(' ');
                i--; // 调整索引，以便下一次循环从正确位置开始
            } else if (ch == '(') {
                stack.push(ch);
            } else if (ch == ')') {
                // 将栈中的元素弹出直到遇到 '('
                while (!stack.isEmpty() && stack.peek() != '(') {
                    postfix.append(stack.pop()).append(' ');
                }
                stack.pop(); // 弹出 '('
            } else if (isOperator(ch)) {
                // 当栈不为空且当前运算符的优先级小于等于栈顶运算符的优先级时，弹出栈顶运算符并加入后缀表达式
                while (!stack.isEmpty() && precedence(stack.peek()) >= precedence(ch)) {
                    postfix.append(stack.pop()).append(' ');
                }
                stack.push(ch); // 将当前运算符入栈
            }
        }

        // 将栈中剩余的运算符全部加入后缀表达式
        while (!stack.isEmpty()) {
            postfix.append(stack.pop()).append(' ');
        }

        return postfix.toString().trim(); // 返回后缀表达式
    }

    // 计算后缀表达式
    public static double evaluatePostfix(String postfix) {
        Stack<Double> stack = new Stack<>();

        for (int i = 0; i < postfix.length(); i++) {
            char ch = postfix.charAt(i);

            if (Character.isDigit(ch)) {
                // 处理多位数字和小数
                StringBuilder number = new StringBuilder();
                while (i < postfix.length() && (Character.isDigit(postfix.charAt(i)) || postfix.charAt(i) == '.')) {
                    number.append(postfix.charAt(i++));
                }
                stack.push(Double.parseDouble(number.toString())); // 将数字入栈
                i--; // 调整索引，以便下一次循环从正确位置开始
            } else if (isOperator(ch)) {
                double b = stack.pop();
                double a = stack.pop();
                // 根据运算符进行计算并将结果入栈
                switch (ch) {
                    case '+': stack.push(a + b); break;
                    case '-': stack.push(a - b); break;
                    case '*': stack.push(a * b); break;
                    case '/': stack.push(a / b); break;
                }
            }
        }

        return stack.pop(); // 返回计算结果
    }

    // 判断是否是运算符
    public static boolean isOperator(char ch) {
        return ch == '+' || ch == '-' || ch == '*' || ch == '/';
    }

    // 返回运算符优先级
    public static int precedence(char ch) {
        switch (ch) {
            case '+':
            case '-': return 1;
            case '*':
            case '/': return 2;
        }
        return -1; // 如果不是运算符，则返回 -1
    }
}

输入：3*(1+2)
输出：

后缀表达式: 3 1 2 + *
计算结果: 9

栈在计算后缀表达式结果时的步骤：

• 1.创建一个空栈，用于存储操作数。
• 2.从左到右遍历后缀表达式的每个字符。
• 3.如果当前字符是操作数（数字），则将其转换为对应的数值，并压入栈中。
• 4.如果当前字符是运算符（+、-、*、/）：
        从栈中弹出两个操作数，分别记为 a 和 b（注意：b 是栈顶元素，a 是次顶元素）。
        根据当前运算符进行计算：根据后缀表达式的特性，b 是操作符 a 的右操作数，a 是左操作数。
• 5.将计算结果压入栈中。
• 6.遍历完后缀表达式后，栈中剩余的唯一元素即为最终的计算结果。

计算过程动画演示：

③、语法解析

括号匹配

import java.util.Stack;

public class TestA {

    public static void main(String[] args) {
        String s = "{[(1234)]}";
        // 调用isValid方法并输出结果，应该输出true，因为输入的括号字符串是有效的
        System.out.println(isValid(s)); // 输出: true
    }

    // 判断括号字符串是否有效的方法
    public static boolean isValid(String s) {
        // 创建一个栈来存放左括号
        Stack<Character> stack = new Stack<>();

        // 遍历输入的字符串中的每一个字符
        for (char c : s.toCharArray()) {
            // 如果是左括号，则压入栈中
            if (c == '(' || c == '{' || c == '[') {
                stack.push(c);
            } else if (c == ')' || c == '}' || c == ']') { // 只处理右括号
                // 如果是右括号且栈为空，说明没有匹配的左括号，返回false
                if (stack.isEmpty()) return false;

                // 弹出栈顶的左括号
                char top = stack.pop();
                // 判断栈顶的左括号和当前的右括号是否匹配，如果不匹配，返回false
                if (c == ')' && top != '(' || c == '}' && top != '{' || c == ']' && top != '[') {
                    return false;
                }
            }
        }

        // 如果栈为空，说明所有的括号都匹配，返回true；否则返回false
        return stack.isEmpty();
    }
}

④、栈排序

用一个栈对数据进行排序

import java.util.*;

public class TestA {

    public static void main(String[] args) {
        // 创建一个LinkedList并添加一些整数元素
        List<Integer> intCollection = new ArrayList<>();
        intCollection.add(5);
        intCollection.add(6);
        intCollection.add(3);
        intCollection.add(1);
        intCollection.add(2);
        intCollection.add(4);

        // 输出排序前的整数集合
        System.out.println("整数集合排序前: " + intCollection);
        // 调用sortCollection方法对集合进行排序
        Collection<Integer> sortedIntCollection = sortCollection(intCollection);
        // 输出排序后的整数集合
        System.out.println("整数集合排序后: " + sortedIntCollection);

    }

    // 对集合进行排序的方法，使用泛型并要求元素实现Comparable接口
    public static <T extends Comparable<T>> Collection<T> sortCollection(Collection<T> collection) {
        // 创建一个栈用于排序
        Stack<T> stack = new Stack<>();
        // 将集合中的元素压入栈中
        for (T element : collection) {
            stack.push(element);
        }

        // 创建一个临时栈用于辅助排序
        Stack<T> tempStack = new Stack<>();
        // 当输入栈不为空时进行排序
        while (!stack.isEmpty()) {
            // 弹出输入栈的栈顶元素
            T temp = stack.pop();
            // 将临时栈中所有大于temp的元素弹出并压入输入栈
            while (!tempStack.isEmpty() && tempStack.peek().compareTo(temp) < 0) {
                stack.push(tempStack.pop());
            }
            // 将temp压入临时栈
            tempStack.push(temp);
        }

        // 将临时栈中的元素全部弹出并存入一个新集合
        Collection<T> sortedCollection = new LinkedList<>();
        while (!tempStack.isEmpty()) {
            sortedCollection.add(tempStack.pop());
        }

        return sortedCollection;
    }
}

⑤、实现特殊算法

深度优先搜索（DFS）
二叉树的非递归前序遍历

回溯算法
例如求解迷宫问题、N皇后问题等。
算法类的暂时先不在这边篇文章内写了。后续会单独再写一些相关的内容。

补充: Stack的方法区别

方法	描述	能否添加 null	会否抛出异常
add	向栈中添加元素	是	不会抛出异常
push	将元素压入栈顶	是	不会抛出异常
peek	查看栈顶元素但不移除	-	如果栈为空，抛出 EmptyStackException
pop	移除并返回栈顶元素	-	如果栈为空，抛出 EmptyStackException